Many people suffer with this problem solving paradigm called Dynamic Programming, one breakthrough I have made in this topic is thinking in top-down manner rather than bottom-up.

DP can be summarized in following equation

Bruteforce + memoization = DP

The Bruteforce Part

Whenever you think about recursion you think of function getting pushed and popped in the stack, that is the proper image of recursion but not the correct way of thinking about when deriving a recursive algorithm. The way I imagine is in terms of function, where I have super parallel computer. Whenever I write a recurrence, suppose F(n-1) + F(n-2) , I imagine that the universe have branched off into two parallel universe where in one universe F(n-1) is calculated and in other F(n-2) then adding them together.

Motivation Problem

There are N students standing in a line. The first student gets 1 chocolate. The second student gets 2 chocolates. The third student however demands that he gets twice as many chocolates as the first student plus the number of chocolate that the second student got. Similarly, the fourth student said that he wanted twice the amount of chocolate that the second student got plus the amount the third student got. Thus, each student wants the amount that the previous student got plus twice the amount the student before that had got. We need to find the total number of chocolate that given to the ‘x’ th student

Lets denote F(x) as the amount of chocolate the x th students got. The x th student demands the amount of chocolate x-1 th student plus twice the chocolate of x-2 th person. In terms of function it could be defined as F(x) = F(x-1) + 2 * F(x-2) .

Boom! We are done.

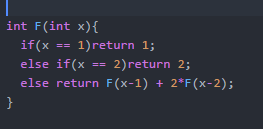
We can memoize the bruteforce recursive code to reduce the time complexity from exponential to polynomial. This part is left as an exercise to the reader.

Going Further

Till now we have discussed basic recurrence. We can have more complex recurrence involving more than one parameter. Read my previous blogs and answer on Quora for further knowledge.

1. https://qr.ae/TW8c67
2. https://qr.ae/TW8EO1

Reduce to One

Problem statement – https://www.codechef.com/MAY19B/problems/REDONE

It doesn’t matter whichever element we choose, answer will be same. I have come to this conclusion after observation on few testcases. Formal proof will be added later.

#include <bits/stdc++.h>
using namespace std;
#define int long long
#define FOR(i,s,e) for(int i=s; i<=e; i++)
#define WL(t) while(t--)
#define MAXN 1000010
#define MOD 1000000007
int dp[MAXN];
int n;
class fastio {
public:
    fastio() {
        ios_base::sync_with_stdio(false);
        cout.tie(nullptr);
        cin.tie(nullptr);
    }
} __fastio;
void precalculate() {
    dp[1] = 1;
    FOR(i,2,MAXN) {
        dp[i] = (dp[i-1] * i + dp[i-1] + i) % MOD;
    }
}
void solve() {
    cin >> n;
    cout << dp[n] << endl;
}
int32_t main() {
  __fastio;
  precalculate();
  int t; cin >> t;
  WL(t) {
    solve();
  }
  return 0;
}

Problem Statement – https://atcoder.jp/contests/dp/tasks/dp_b

This problem is similar to Frog – 1, but this time from ‘i’ we could jump to i+1, i+2, … i+K , few changes in the previous code is needed.

Implementation

#include <bits/stdc++.h>
using namespace std;
#define MAXN 100010
#define INF 1e9
#define FOR(i,s,e) for(int i=s; i<=e; i++)
int cost[MAXN], memo[MAXN];
int n, k;
class fastio {
public:
    fastio() {
        ios_base::sync_with_stdio(false);
        cout.tie(nullptr);
        cin.tie(nullptr);
    }
} __fastio;
int f(int i) {
    if(i > n) return INF;
    if(i == n) return 0;
    if(memo[i] != -1) return memo[i];
    else {
        int ans = INF;
        FOR(j,1,k) {
            ans = min(ans, f(i+j) + abs(cost[i] - cost[i+j]));
        }
        return memo[i] = ans;
    }
}
void solve() {
    cin >> n >> k;
    FOR(i,1,n) {
        cin >> cost[i];
    }
    memset(memo, -1, sizeof(memo));
    cout << f(1) << endl;
}
int main() {
  __fastio;
  solve();
  return 0;
}

Problem – https://atcoder.jp/contests/dp/tasks/dp_a

At every instance we have two choices, i.e either jump to ‘i+1’ th or ‘i+2’ th rock, and the cost of jumping for the former is |cost[i] – cost[i+1]| and for the latter it’s |cost[i] – cost[i+2]| and minimum of them is the answer, therefore the recurrence relation would be.

min{f(i+1) + |cost[i] – cost[i+1]| , f(i+2) + |cost[i] – cost[i+2]|}

Here, |x| denotes absolute value of ‘x’

The implementation is rather straight forward.

#include <bits/stdc++.h>
using namespace std;
#define MAXN 100010
#define INF 1e9
#define FOR(i,s,e) for(int i=s; i<=e; i++)
int cost[MAXN], memo[MAXN];
int n;
class fastio {
public:
    fastio() {
        ios_base::sync_with_stdio(false);
        cout.tie(nullptr);
        cin.tie(nullptr);
    }
} __fastio;
int f(int i) {
    if(i > n) return INF;
    if(i == n) return 0;
    if(memo[i] != -1) return memo[i];
    return memo[i] = min(f(i+1) + abs(cost[i] - cost[i+1]), f(i+2) + abs(cost[i] - cost[i+2]));
}
void solve() {
    cin >> n;
    FOR(i,1,n) {
        cin >> cost[i];
    }
    memset(memo, -1, sizeof(memo));
    cout << f(1) << endl;
}
int main() {
  __fastio;
  solve();
  return 0;
}